The dining philosophers problem is invented by E. W. Dijkstra. Imagine that five philosophers who spend their lives just thinking and easting. In the middle of the dining room is a circular table with five chairs. The table has a big plate of spaghetti. However, there are only five chopsticks available, as shown in the following figure. Each philosopher thinks. When he gets hungry, he sits down and picks up the two chopsticks that are closest to him. If a philosopher can pick up both chopsticks, he eats for a while. After a philosopher finishes eating, he puts down the chopsticks and starts to think.
On the previous page we saw a solution in which each philosopher picks his left chopstick followed by his right chopstick. We pointed out there that that solution could cause deadlock and have the starvation problem. Here, we shall present a solution that still uses mutex locks but has no deadlock.
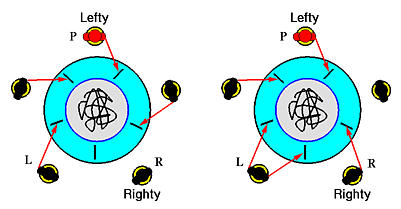
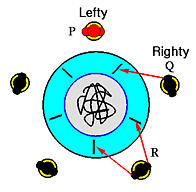
It turns out that eliminating deadlock is not very difficult. In our previous solution, the deadlock is caused by having every philosopher to pick up his left chopstick. This produces a circular waiting. If this circular waiting can be broken, deadlocks will go away. To this end, we can force on of the philosophers to act differently. More precisely, we can force a philosopher to pick up his right chopstick first followed by his left chopstick. A philosopher who picks up his left chopstick followed by his right chopstick is referred to as a lefty; otherwise, he is a righty. Note that the sum of lefty and righty philosophers must be equal to the number of philosophers and both cannot be zero. Intuitively, the existence of a righty philosopher can break the circular waiting, we saw in the previous example. But, is it really the case?
Recall that a deadlock occurs if some or all of the threads are involved in a circular waiting. As long as we can show that such circular waiting will not occur, the system will have no deadlock. In the following, we assume there is only one righty philosopher. It is not difficult to extend the following discussion to the case of multiple righty philosophers. We shall pick an arbitrary philosopher and show that he has a chance to pick up both chopsticks and eat. This chosen philosopher, say P, can be a lefty or a righty. The following analysis is certainly not the shortest one, but, we believe it is easy to understand.
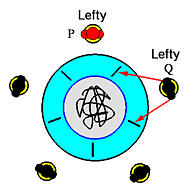
If P's right neighbor, say Q, is not eating, Q las his left chopstick (i.e., P's right chopstick) and is waiting for his right chopstick as shown in the figure below. The worst case is that Q's right chopstick is being held by Q's right neighbor. This situation can spread to P's left neighbor. In this case, P's left neighbor has both chopsticks and can eat. As a result, once P's left neighbor puts down his chopsticks, everyone except P has a chance to pick up his right chopstick and eat. As for P, he has a chance to pick up his right chopstick once his right neighbor finishes eating and puts down both chopsticks.

Therefore, we conclude that philosopher P will have a chance to pick up his right chopstick. Because of the previous case, philosopher P eventually can eat unless he is preempted by one of its neighbor. However, this is a starvation rather than a deadlock.
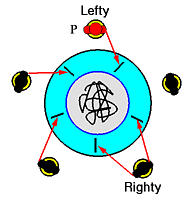
If the righty is eating, he has two chopsticks as shown below. Once the righty finishes eating, he puts down both chopsticks, his left neighbor has a chance to eat, and, as a result, everyone to the left of the righty has a chance to eat. Thus, no deadlock occurs.
This program is very similar to the previous one. However, because there are lefty and righty philosophers, each of these philosophers should have an indicator. To simplify our programming task, we add two variables FirstChopstick and SecondChopstick to store the chopstick numbers. More precisely, a philosopher must pick up chopstick FirstChopstick followed by chopstick SecondChopstick. Variable No is the philosopher number, and char variable Id indicates if this philosopher is a lefty or a righty.
#include "ThreadClass.h"
#define PHILOSOPHERS 5
class Philosopher: public Thread
{
public:
Philosopher(int Number, char id, int iter); // constructor
private:
char Id; // either "lefty" or "righty" philosopher
int No;
int FirstChopstick, // the 1st chopstick to pick up
SecondChopstick; // the 2nd to pick up
int Iteration;
void ThreadFunc();
};
|
| Click here to download this file (lefty-righty.h) |
In the implementation file, we still have a function Filler() for generating a string of spaces. Now let us turn to the constructor. It takes three arguments for the three private variables No, Id and Iteration. If this is a lefty (resp., righty) philosopher, its thread name is Lefty (resp., Righty) followed by its number. Thus, the thread names are Lefty1, Lefty2, ..., Righty3, Righty4. The actual name depends on the main program. For example, if the main program assign philosophers 0, 1, 2, and 3 to be lefty and 4 to be righty, the thread names are Lefty1, Lefty2, Lefty3, Lefty4, Righty5. The constructor also determine the first and second chopsticks to be picked up by a philosopher. For a lefty philosopher, he picks up his left followed by his right chopsticks. Thus, variables FirstChopstick and SecondChopstick are set to No and (No + 1) % PHILOSOPHERS, respectively. For a righty philosopher, the order is reversed. Once this completes, the thread function ThreadFunc() is almost identical to the previous one. The only difference is the use of precomputed FirstChopstick and SecondChopstick.
#include <iostream>
#include "lefty-righty.h"
extern Mutex *Chopstick[PHILOSOPHERS];
strstream *Filler(int n)
{
int i;
strstream *Space;
Space = new strstream;
for (i = 0; i < n; i++)
(*Space) << ' ';
(*Space) << '\0';
return Space;
}
Philosopher::Philosopher(int Number, char id, int iter)
: No(Number), Id(id), Iteration(iter)
{
ThreadName.seekp(0, ios::beg);
if (Id == 'L') { // lefties have No followed No+1
ThreadName << "Lefty" << Number + 1 << '\0';
FirstChopstick = No;
SecondChopstick = (No + 1) % PHILOSOPHERS;
}
else { // righties have No+1 followed by No
ThreadName << "Righty" << Number + 1 << '\0';
FirstChopstick = (No + 1) % PHILOSOPHERS;
SecondChopstick = No;
}
}
void Philosopher::ThreadFunc()
{
Thread::ThreadFunc();
strstream *Space;
int i;
Space = Filler(No*2);
for (i = 0; i < Iteration; i++) {
Delay();
Chopstick[FirstChopstick]->Lock();
Chopstick[SecondChopstick]->Lock(); // gets two chopsticks
cout << Space->str() << ThreadName.str() << " begin eating." << endl;
Delay();
cout << Space->str() << ThreadName.str() << " finish eating." << endl;
Chopstick[FirstChopstick]->Unlock(); // release 2 chopstick
Chopstick[SecondChopstick]->Unlock();
}
Exit(); // thread terminates
}
|
| Click here to download this file (lefty-righty.cpp) |
The main program requires two command line arguments. The first one gives how many lefty philosophers, and the second indicates the number thinking-eating cycles. Note that because we have 5 philosophers, the number of lefty philosophers must be less than 5 so that there will be at least one righty philosophers to break the circular waiting that causes a deadlock. As in the previous example, we first create all mutex locks for protecting the chopsticks. Then, the philosophers are created and the first few are assigned as lefty philosophers. After a philosopher is created, it is run by calling the method Begin(). Finally, the main thread waits for the completion of its child threads, and then exit.
#include <iostream>
#include <stdlib.h>
#include "lefty-righty.h"
Mutex *Chopstick[PHILOSOPHERS];
int main(int argc, char *argv[])
{
Philosopher *philosopher[PHILOSOPHERS];
int i;
int n;
strstream name;
if (argc != 3) {
cout << "Usage " << argv[0] << " #-of-lefty " <<
" #-of-iterations." << endl;
exit(-1);
}
else {
n = abs(atoi(argv[1]));
if (n >= PHILOSOPHERS) { // make sure # of lefties are valid
cout << "The number of lefty philosophers MUST be less than "
<< PHILOSOPHERS << endl;
exit(-1);
}
Iteration = abs(atoi(argv[2]));
}
// initialize chopstick mutexs
for (i = 0; i < PHILOSOPHERS; i++) {
name.seekp(0, ios::beg);
name << "ChopStick" << i << '\0';
Chopstick[i] = new Mutex(name.str());
}
// fire up both righty and lefty philosophers threads
for (i = 0; i < PHILOSOPHERS; i++) {
if (i < n) // it's a lefty philosopher
philosopher[i] = new Philosopher(i, 'L', Iteration);
else // it's a righty philosopher
philosopher[i] = new Philosopher(i, 'R', Iteration);
philosopher[i]->Begin();
}
// wait for all philosopher threads
for (i=0; i < PHILOSOPHERS; i++)
philosopher[i]->Join();
Exit();
return 0;
}
|
| Click here to download this file (lefty-righty-main.cpp) |
We showed that this solution does not have deadlock. How about starvation? It could cause starvation. We saw this possibility informally in the discussion above. However, we can easily see that the starvation example shown in the previous example also works for this deadlock-free version. Will you be able to find more subtle and more complicated starvation examples? Please try it.


|

|

|