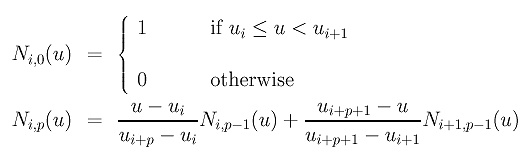

Bézier basis functions are used as weights. B-spline basis functions will be used the same way; however, they are much more complex. There are two interesting properties that are not part of the Bézier basis functions, namely: (1) the domain is subdivided by knots, and (2) basis functions are not non-zero on the entire interval. In fact, each B-spline basis function is non-zero on a few adjacent subintervals and, as a result, B-spline basis functions are quite "local".
Let U be a set of m + 1 non-decreasing numbers, u0 <= u2 <= u3 <= ... <= um. The ui's are called knots, the set U the knot vector, and the half-open interval [ui, ui+1) the i-th knot span. Note that since some ui's may be equal, some knot spans may not exist. If a knot ui appears k times (i.e., ui = ui+1 = ... = ui+k-1), where k > 1, ui is a multiple knot of multiplicity k, written as ui(k). Otherwise, if ui appears only once, it is a simple knot. If the knots are equally spaced (i.e., ui+1 - ui is a constant for 0 <= i <= m - 1), the knot vector or the knot sequence is said uniform; otherwise, it is non-uniform.
The knots can be considered as division points that subdivide the interval [u0, um] into knot spans. All B-spline basis functions are supposed to have their domain on [u0, um]. In this note, we use u0 = 0 and um = 1 frequently so that the domain is the closed interval [0,1].
To define B-spline basis functions, we need one more parameter, the degree of these basis functions, p. The i-th B-spline basis function of degree p, written as Ni,p(u), is defined recursively as follows:
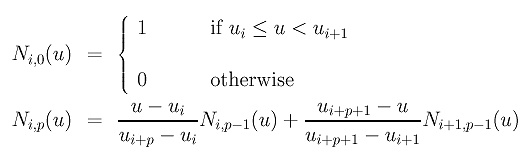
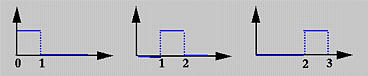
The above is usually referred to as the Cox-de Boor recursion formula. This definition looks complicated; but, it is not difficult to understand. If the degree is zero (i.e., p = 0), these basis functions are all step functions and this is what the first expression says. That is, basis function Ni,0(u) is 1 if u is in the i-th knot span [ui, ui+1). For example, if we have four knots u0 = 0, u1 = 1, u2 = 2 and u3 = 3, knot spans 0, 1 and 2 are [0,1), [1,2), [2,3) and the basis functions of degree 0 are N0,0(u) = 1 on [0,1) and 0 elsewhere, N1,0(u) = 1 on [1,2) and 0 elsewhere, and N2,0(u) = 1 on [2,3) and 0 elsewhere. This is shown below:
To understand the way of computing Ni,p(u) for p greater than 0, we use the triangular computation scheme. All knot spans are listed on the left (first) column and all degree zero basis functions on the second. This is shown in the following diagram.
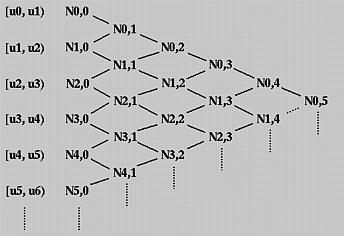
To compute Ni,1(u), Ni,0(u) and Ni+1,0(u) are required. Therefore, we can compute N0,1(u), N1,1(u), N2,1(u), N3,1(u) and so on. All of these Ni,1(u)'s are written on the third column. Once all Ni,1(u)'s have been computed, we can compute Ni,2(u)'s and put them on the fourth column. This process continues until all required Ni,p(u)'s are computed.
In the above, we have obtained N0,0(u), N1,0(u) andN2,0(u) for the knot vector U = { 0, 1, 2, 3 }. Let us compute N0,1(u) and N1,1(u). To compute N0,1(u), since i = 0 and p = 1, from the definition we have
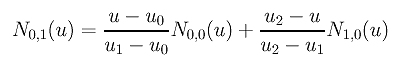
Since u0 = 0, u1 = 1 and u2 = 2, the above becomes
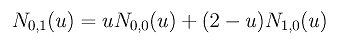
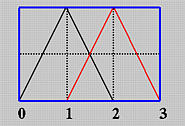
Since N0,0(u) is non-zero on [0,1) and N1,0(u) is non-zero on [1,2), if u is in [0,1) (resp., [1,2) ), only N0,0(u) (resp., N1,0(u) ) contributes to N0,1(u). Therefore, if u is in [0,1), N0,1(u) is uN0,0(u) = u, and if u is in [1,2), N0,1(u) is (2 - u)N1,0(u) = (2 - u). Similar computation gives N1,1(u) = u - 1 if u is in [1,2), and N1,1(u) = 3 - u if u is in [2,3). In the following figure, the black and red lines are N0,1(u) and N1,1(u), respectively. Note that N0,1(u) (resp., N1,1(u)) is non-zero on [0,1) and [1,2) (resp., [1,2) and [2,3)).
Once N0,1(u) and N1,1(u) are available, we can compute N0,2(u). The definition gives us the following:
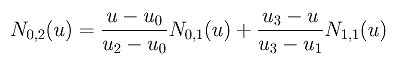
Plugging in the values of the knots yields

Note that N0,1(u) is non-zero on [0,1) and [1,2) and N1,1(u) is non-zero on [1,2) and [2,3). Therefore, we have three cases to consider:
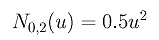
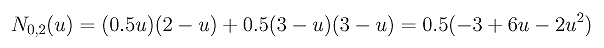
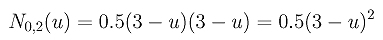
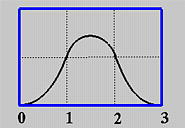

Since Ni,1(u) is computed from Ni,0(u) and Ni+1,0(u) and since Ni,0(u) and Ni+1,0(u) are non-zero on span [ui, ui+1) and [ui+1, ui+2), respectively, Ni,1(u) is non-zero on these two spans. In other words, Ni,1(u) is non-zero on [ui, ui+2). Similarly, since Ni,2(u) depends on Ni,1(u) and Ni+1,1(u) and since these two basis functions are non-zero on [ui, ui+2) and [ui+1, ui+3), respectively, Ni,2(u) is non-zero on [ui, ui+3). In general, to determine the non-zero domain of a basis function Ni,p(u), one can trace back using the triangular computation scheme until it reaches the first column. The covered spans are the non-zero domain of this basis function. For example, suppose we want to find out the non-zero domain of N1,3(u). Based on the above discussion, we can trace back in the north-west and south-west directions until the first column is reached as shown with the blue dotted line in the following diagram. Thus, N1,3(u) is non-zero on [u1, u2), [u2, u3), [u3, u4) and [u4, u5). Or, equivalently, it is non-zero on [u1, u5).
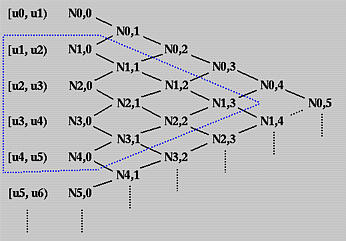
In summary, we have the following observation:
Basis function Ni,p(u) is non-zero on [ui, ui+p+1). Or, equivalently, Ni,p(u) is non-zero on p+1 knot spans [ui, ui+1), [ui+1, ui+2), ..., [ui+p, ui+p+1).
Next, we shall look at the opposite direction. Given a knot span [ui, ui+1), we want to know which basis functions will use this span in its computation. We can start with this knot span and draw a north-east bound arrow and a south-east bound arrow. All basis functions enclosed in this wedge shape use Ni,0(u) (why?) and hence are non-zero on this span. Therefore, all degree p basis functions that are non-zero on [ui, ui+1) are the intersection of this wedge and the column that contains all Ni,p(u)'s. In fact, this column and the two arrows form an equilateral triangle with this column being the vertical side. Counting from Ni,0(u) to Ni,p(u) there are p+1 columns. Therefore, the vertical side of the equilateral triangle must have at most p+1 entries, namely Ni,p(u), Ni-1,p(u), Ni-2,p(u), ..., Ni-p+2,p(u), Ni-p+1,p(u) and Ni-p,p(u).
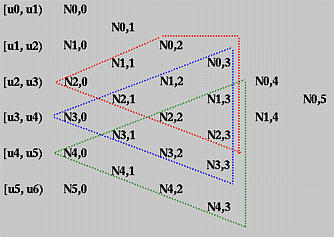
Let us take a look at the above diagram. To find all degree 3 basis functions that are non-zero on [u4, u5), draw two arrows and all functions on the vertical edges are what we want. In this case, they are N1,3(u), N2,3(u), N3,3(u), and N4,3(u). This is shown with the orange triangle. The blue (resp., red) triangle shows the degree 3 basis functions that are non-zero on [u3, u4) (resp., [u2, u3) ). Note that there are only three degree three basis polynomials that are non-zero on [u2, u3).
In summary, we have observed the following property.
On any knot span [ui, ui+1), at most p+1 degree p basis functions are non-zero, namely: Ni-p,p(u), Ni-p+1,p(u), Ni-p+2,p(u), ..., Ni-1,p(u) and Ni,p(u),

