

Once a polyhedron model is available one might want to edit it by adding or deleting vertices, edges and faces to create a new polyhedron. These operations are called Euler Operators. However, it has been shown that in the process of editing a polyhedron with Euler operators, some intermediate results may not be valid solids at all.
Recall from the discussion of the Euler-Poincaré formula that the following holds for all polyhedra:
where V, E, F, L, S and G are the numbers of vertices, edges, faces, loops, shells and genus, respectively. Based on this relation, some Euler operators have been selected for editing a polyhedron so that the Euler-Poincaré formula is always satisfied. There are two groups of such operators: the Make group and the Kill group. Operators start with M and K are operators of the Make and Kill groups, respectively.
Euler operators are written as Mxyz and Kxyz for operations in the Make and Kill groups, respectively, where x, y and z are elements of the model (e.g., a vertex, edge, face, loop, shell and genus). For example, MEV means adding an edge and a vertex while KEV means deleting an edge and a vertex.
It has been proved by Mantyla in 1984 that Euler operators form a complete set of modeling primitives for manifold solids. More precisely, every topologically valid polyhedron can be constructed from an initial polyhedron by a finite sequence of Euler operators. Therefore, Euler operators are powerful operations.

| Operator Name | Meaning | V | E | F | L | S | G |
| MEV | Make an edge and a vertex | +1 | +1 | |
|
|
|
| MFE | Make a face and an edge | |
+1 | +1 | +1 | |
|
| MSFV | Make a shell, a face and a vertex | +1 | |
+1 | +1 | +1 | |
| MSG | Make a shell and a hole | |
|
|
|
+1 | +1 |
| MEKL | Make an edge and kill a loop | |
+1 | |
-1 | |
|
The above table shows the change of values of V, E, F, L, S and G. Note that adding a face produces a loop, the outer loop of that face. Therefore, when F is increased, L should also be increased. This new loop and the new face will cancel each other in the subexpression L - F. Please verify that none of these operators would cause the Euler-Poincaré formula to fail.
The following table illustrates the way of using Euler operators to construct a tetrahedron. Vertices, edges, and faces are in red, blue and green; the only shell is in transparent gray. The first step uses MSFV to obtain a shell with a face and a vertex. The next three steps use MEVs, each of which adds an edge and a vertex. The last three steps use MFE, each of which adds a face and an edge. Thus, in seven steps or seven Euler operators a tetrahedron is constructed.
| Operator Name | Meaning | V | E | F | L | S | G | Result |
| MSFV | Make a shell, a face and a vertex | +1 | |
+1 | +1 | +1 | |
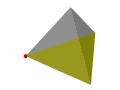 |
| MEV | Make an edge and a vertex | +1 | +1 | |
|
|
|
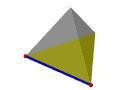 |
| MEV | Make an edge and a vertex | +1 | +1 | |
|
|
|
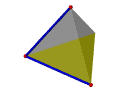 |
| MEV | Make an edge and a vertex | +1 | +1 | |
|
|
|
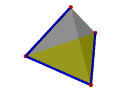 |
| MFE | Make a face and an edge | |
+1 | +1 | |
+1 | |
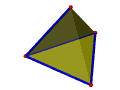 |
| MFE | Make a face and an edge | |
+1 | +1 | |
+1 | |
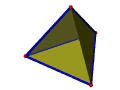 |
| MFE | Make a face and an edge | |
+1 | +1 | |
+1 | |
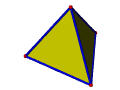 |
MSG simply makes a shell with a hole. After this, one can add vertices, edges, faces, loops. There must be loops, because the new hole penetrates at least one face.
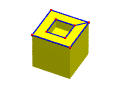
MEKL makes an edge and at the same time kills a loop. A commonly used MEKL is adding an edge connecting the outer loop and the inner loop of a face. In this case, the number of edges E is increased by 1 and the number of loops L is decreased by 1 since that loop is killed. The left figure below shows two loops of the top face while the right one shows the new edge added after performing a MEKL. Thus, the inner and outer are "joint" together with the new edge becoming a single face.
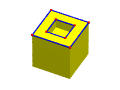

| Operator Name | Meaning | V | E | F | L | S | G |
| KEV | Kill an edge and a vertex | -1 | -1 | |
|
|
|
| KFE | Kill a face and an edge | |
-1 | -1 | -1 | |
|
| KSFV | Kill a shell, a face and a vertex | -1 | |
-1 | -1 | -1 | |
| KSG | Kill a shell and a hole | |
|
|
|
-1 | -1 |
| KEML | Kill an edge and make a loop | |
-1 | |
+1 | |
|
With these operators, one can start with a tetrahedron and reduce it to nothing. Since these operators are the opposites of the Make operators, we shall not go further here.